Basic Trigonometry and Vector Functions for PHY 100
Print this page for your reference

Click here for more help on Right Angle functions

	I would like for you to know sine, cosine, and tangent for the angles of θ = 0°, 30°, 45°, 60°, and 90°. sin(θ) = Y/R cos(θ) = X/R tan(θ) = Y/X R2 = X2 + Y2 R = √(X2 + Y2)
sin(0°) = 0.0 cos(0°) = 1.0 tan(0°) = 0.0 sin(30°) = 0.5 cos(30°) = 0.866 tan(30°) = 0.577 sin(45°) = 0.707 cos(45°) = 0.707 tan(45°) = 1.0 sin(60°) = 0.866 cos(60°) = 0.5 tan(60°) = 1.732 sin(90°) = 1.0 cos(90°) = 0.0 tan(90°) = ∞

Examples:

4 x cos(30°) = 4 x 0.866 = 3.464
1 / sin(30°) = 1 / 0.5 = 2.0
cos(45°) / sin(45°) = 0.707 / 0.707 = 1.0

Vectors:

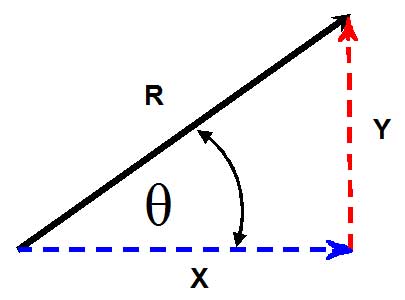
So, if R is a vector, then R is the sum of vectors X and Y.  That is 

Examples:

1)   A vector with magnitude 10m at 60°.  What are the magnitudes of the components or rather the lengths of the legs?
     Answer: 
     X = 10m x cos(60°) = 10m x 0.5 = 5m
     Y = 10m x sin(60°) = 10m x 0.866 = 8.66m

2) If the components of a vector are X = 5m and Y = 8.66m, what is the magnitude of the vector?
    Answer:
    Using R² = X² + Y², we have R = √(X² + Y²) = √(5² + 8.66²) = √(25 + 75) = √100 = 10m (rounding off)

3) A vector at 45° has a magnitude of 35m.  What is the vertical Y component?
    Answer:
    Y = R x sin(45°) = 35 x 0.707 = 24.7 m  (also, the X component would be 35 x cos(45°) = 35 x 0.707 = 24.7)

The above is the level of trigonometry and vectors that we will use in PHY 100.  In other words, I will ask questions that are only in angles of 0°,30°,45°,60°, and 90°.  You can use a calculator to determine the angles or you can use the table above, whichever is comfortable for you.  

Top